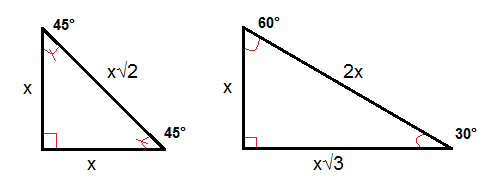
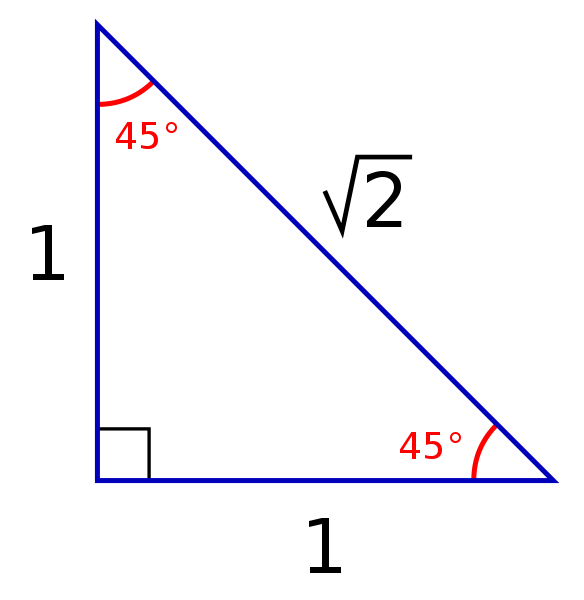
The 45°45°90° triangle, also referred to as an isosceles right triangle, since it has two sides of equal lengths, is a right triangle in which the sides corresponding to the angles, 45°45°90°, follow a ratio of 11√ 2 Like the 30°60°90° triangle, knowing one side length allows you to determine the lengths of the other sidesA 30̊ 60̊ 90̊ right triangle or rightangled triangle is a triangle with angles 30̊ 60̊ 90̊This allows us to find the ratio between each side of the triangle by using the Pythagorean theorem Check it out below!

30 60 90 Triangle 30 Degree Right Angle Transparent Png 1024x592 Free Download On Nicepng
90-60-30 triangle properties
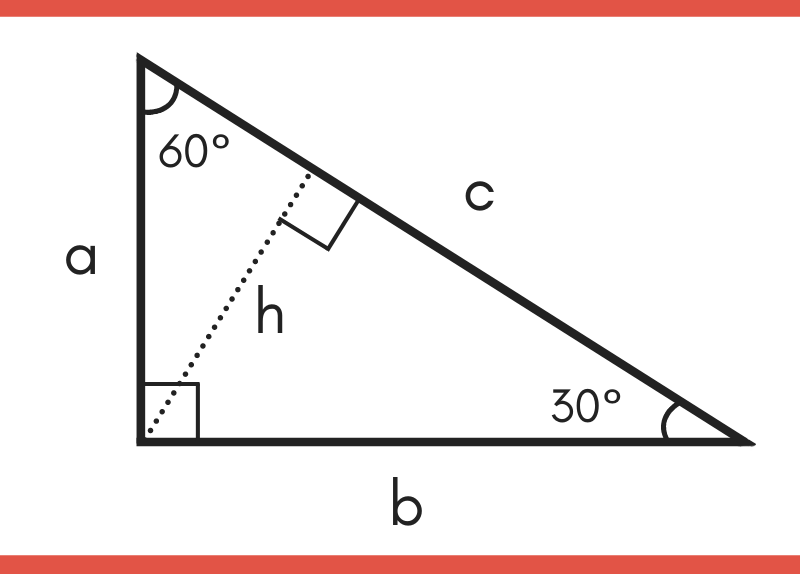
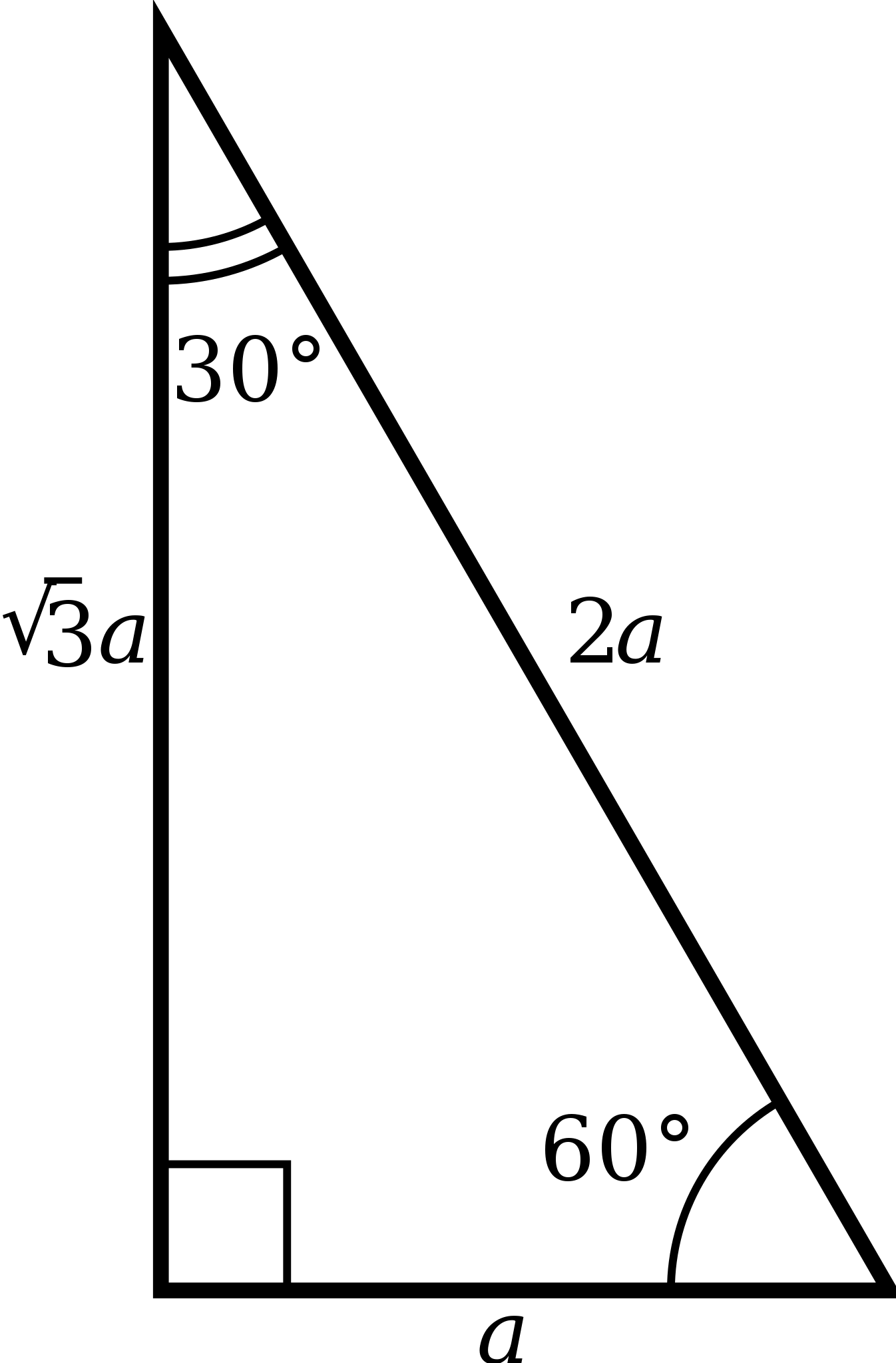
90-60-30 triangle properties-A triangle is a right triangle where the three interior angles measure 30 °, 60 °, and 90 ° Right triangles with interior angles are known as special right triangles Special triangles in geometry because of the powerful relationships that 30 60 90 triangle sides If we know the shorter leg length a, we can find out that b = a√3 c = 2a If the longer leg length b is the one parameter given, then a = b√3/3 c = 2b√3/3 For hypotenuse c known, the legs formulas look as follows a = c/2
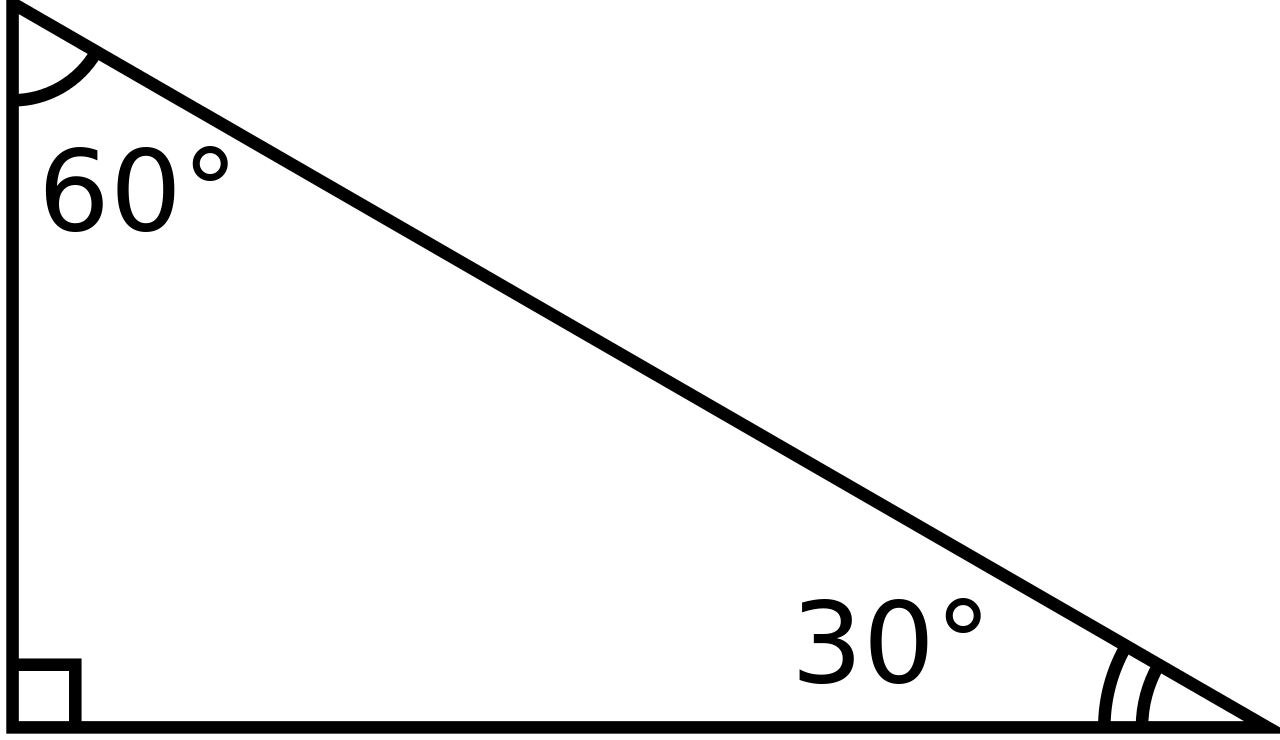



File 30 60 90 Triangle 2 Svg Wikimedia Commons
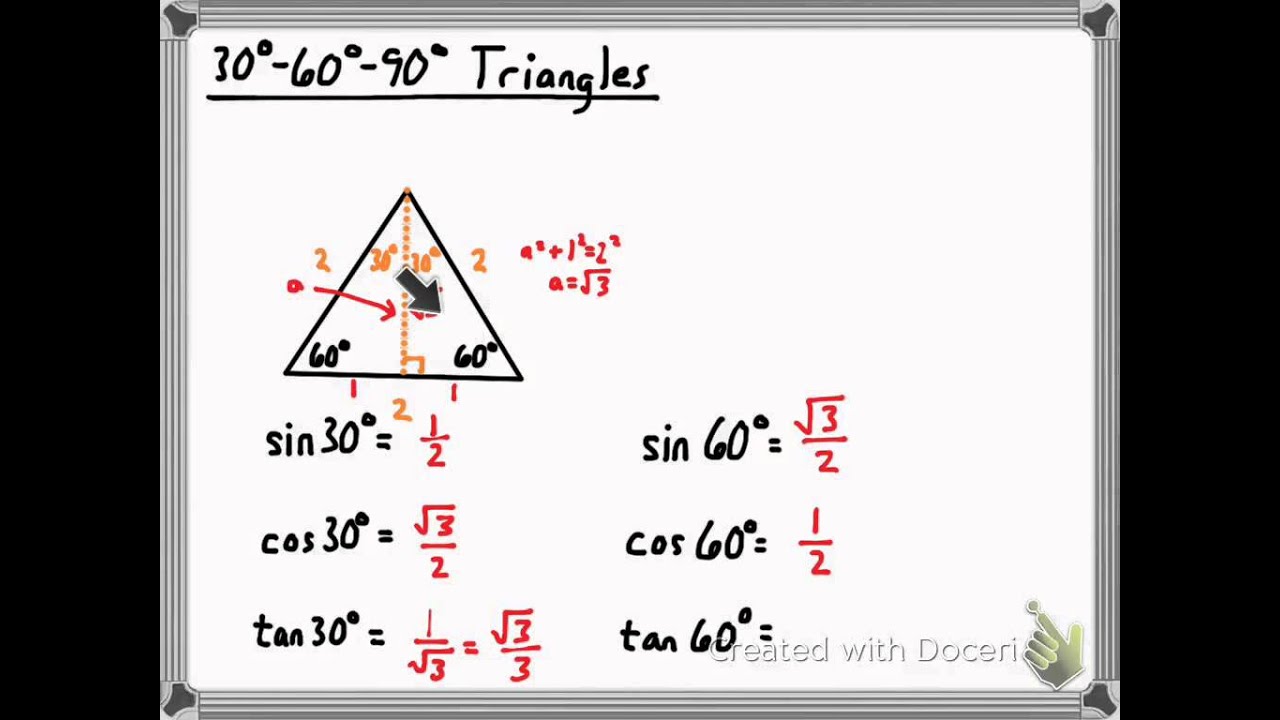
A triangle is a special right triangle (a right triangle being any triangle that contains a 90 degree angle) that always has degree angles of 30 degrees, 60 degrees, and 90 degrees Because it is a special triangle, it also has side length values which are always in a consistent relationship with one anotherUsing what we know about triangles to solve what at first seems to be a challenging problem Created by Sal Khan Special right triangles Special right triangles proof (part 1) Special right triangles proof (part 2) Practice Special right triangles triangle example problem This is the currently selected itemA right triangle (literally pronounced "thirty sixty ninety") is a special type of right triangle where the three angles measure 30 degrees, 60 degrees, and 90 degrees The triangle is significant because the sides exist in an easytoremember ratio 1 √3 3 2 That is to say, the hypotenuse is twice as long as the shorter leg, and
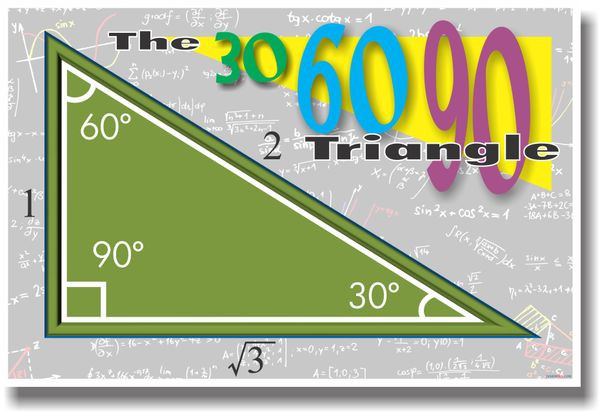
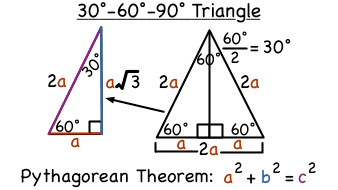
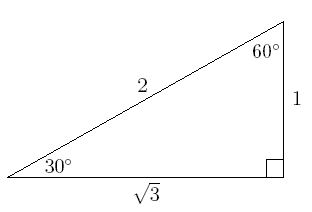
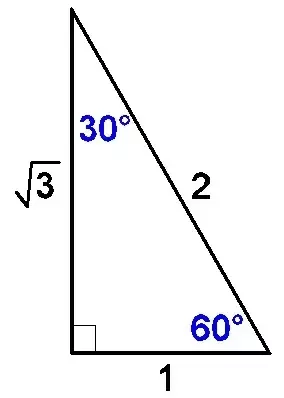
LESSON 3 Prove It (Part 2) LESSON 4 Using the Pythagorean Theorem LESSON 5 Special Right Triangles LESSON 6 30, 60, 90 Triangles LESSON 7 Isosceles Right Triangles LESSON 8 Special Right Triangles Puzzle Activity Objective Discovering Similar Triangles with the Pattern a, a√3, 2a Proving that These Triangles are 30, 60, 90 Triangles A triangle is a right triangle with angles 30^@, 60^@, and 90^@ and which has the useful property of having easily calculable side lengths without use of trigonometric functions A triangle is a special right triangle, so named for the measure of its angles Its side lengths may be derived in the following manner Begin with an equilateral triangle of sideTHE 30°60°90° TRIANGLE THERE ARE TWO special triangles in trigonometry One is the 30°60°90° triangle The other is the isosceles right triangle They are special because, with simple geometry, we can know the ratios of their sides Theorem In a 30°60°90° triangle the sides are in the ratio 1 2 We will prove that below
Transcribed image text On your own paper, draw a 30°60°90° right triangle Label the shortest side a length of 2 (inches);30 60 90 Triangle Figure 1 30 60 90 Triangle The right triangle defined by the three angles , and is a special triangle that has meaningful properties in mathematics General Form The general form of the triangle, shown below, can be given in terms of , where measures the length of the opposite side of the triangle The triangle is a special right triangle, and knowing it can save you a lot of time on standardized tests like the SAT and ACT Because its angles and side ratios are consistent, test makers love to incorporate this triangle into problems, especially on the nocalculator portion of the SAT



30 60 90 Triangle Formulas Rules And Sides Science Trends



Right Triangle Degrees 30 60 90 Clipart Etc
30 60 90 Right Triangle Calculator Short Side a Input one number of input area Long Side b Hypotenuse c Area Perimeter Input one number then click "calculate" button! A triangle is a specific type of right triangle that has angles of 30 and 60 degrees in addition to the 90degree angle of all right triangles TheTriangles are classified as "special right triangles" They are special because of special relationships among the triangle legs that allow one to easily arrive at the length of the sides with exact answers instead of decimal approximations when using trig functions




Amazon Com Triangle Set 10 Inch 30 60 45 90 Office Products
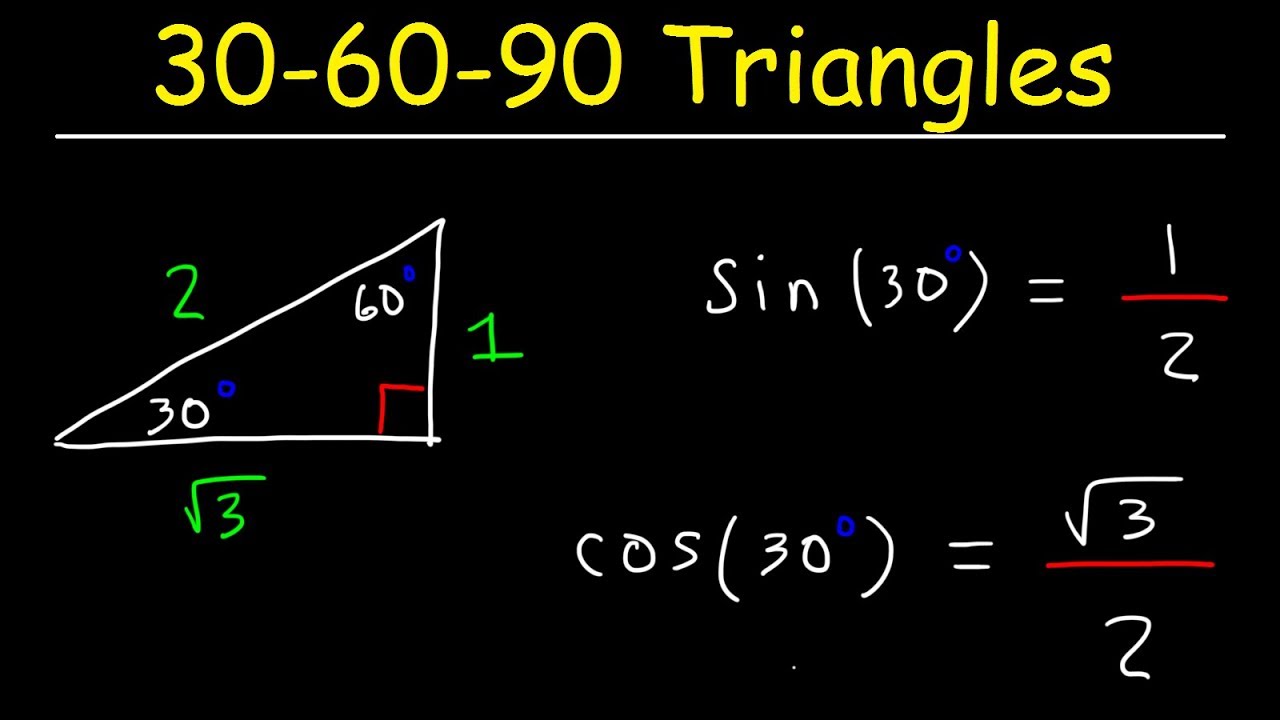



30 60 90 Triangles Special Right Triangle Trigonometry Youtube
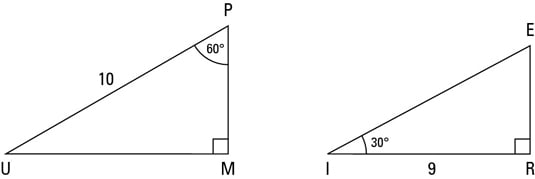
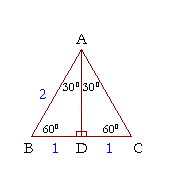
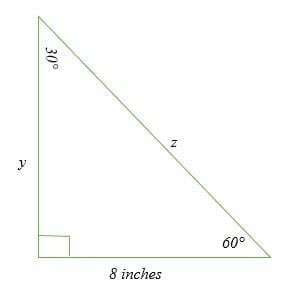
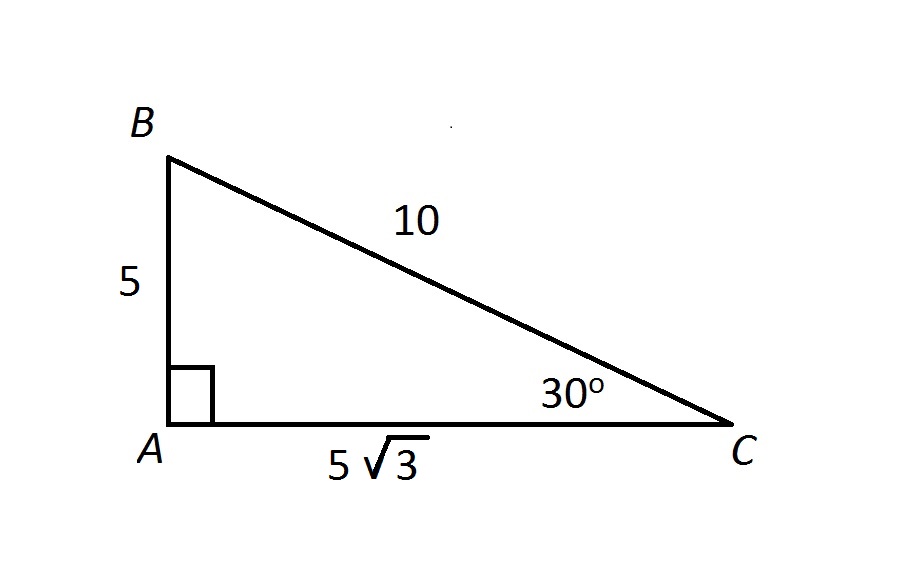
Example of 30 – 60 90 rule Example 1 Find the missing side of the given triangle As it is a right triangle in which the hypotenuse is the double of one of the sides of the triangle Thus, it is called a triangle where smaller angle will be 30 The longer side is always opposite to 60° and the missing side measures 3√3 units inThen ABD is a 30°–60°–90° triangle with hypotenuse of length 2, and base BD of length 1 The fact that the remaining leg AD has length √ 3 follows immediately from the Pythagorean theorem The 30°–60°–90° triangle is the only right triangle whose angles are in an arithmetic progressionMultiply this answer by the square root of 3 to find the long leg Type 3 You know the long leg (the side across from the 60degree angle) Divide this side by the square root of 3 to find the short side Double that figure to find the hypotenuse Finding the other sides of a triangle when you know the hypotenuse



The 30 60 90 Triangle Posterenvy Com



30 60 90 Triangle From Wolfram Mathworld
This page shows to construct (draw) a 30 60 90 degree triangle with compass and straightedge or ruler We are given a line segment to start, which will become the hypotenuse of a right triangle It works by combining two other constructions A 30 degree angle, and a 60 degree angleBecause the interior angles of a triangle always add to 180 degrees, the third angle must be 90 A triangle is a unique right triangle whose angles are 30º, 60º, and 90º The triangle is unique because its side sizes are always in the proportion of 1 √ 32 Any triangle of the kind can be fixed without applying longstep approaches such as the Pythagorean Theorem and trigonometric featuresCheck out this tutorial to learn about triangles!




Triangle Set 8 Inch 30 60 45 90 Walmart Com




30 60 90 Triangle 30 Degree Right Angle Transparent Png 1024x592 Free Download On Nicepng
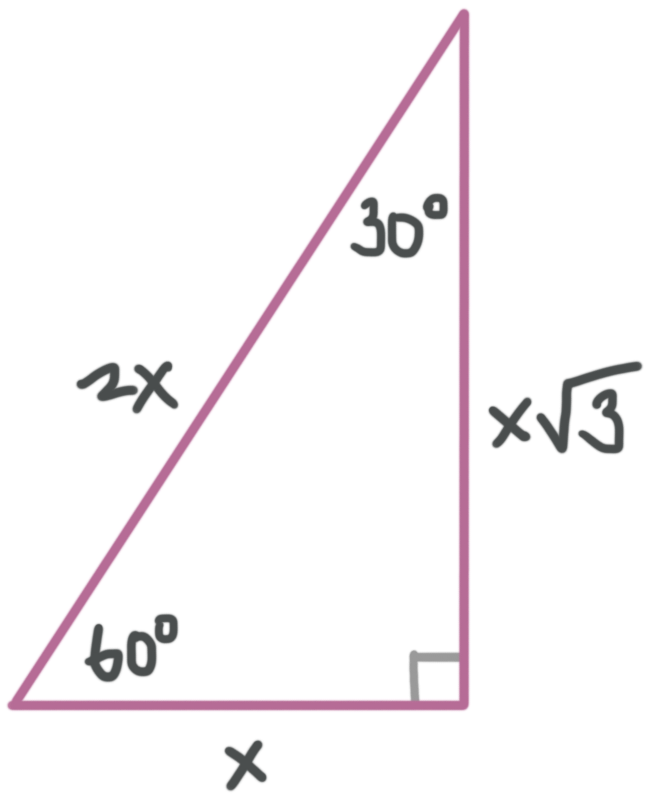
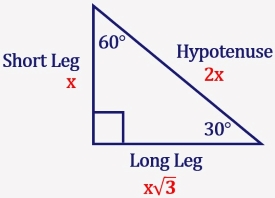
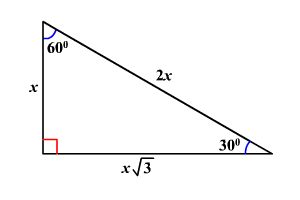
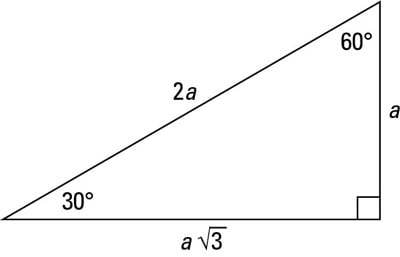
Although all right triangles have special features – trigonometric functions and the Pythagorean theoremThe most frequently studied right triangles, the special right triangles, are the 30, 60, 90 Triangles followed by the 45, 45, 90 trianglesHow to use a special right triangle () to solve problems30°60°90° Triangles There is a special relationship among the measures of the sides of a 30 ° − 60 ° − 90 ° triangle A 30 ° − 60 ° − 90 ° triangle is commonly encountered right triangle whose sides are in the proportion 1 3 2 The measures of the sides are x, x 3, and 2 x



1



The Easy Guide To The 30 60 90 Triangle
Aluminum drafting triangles are a useful tool for educational and professional use Chose from 30°/ 60°/90° or 45°/90° drafting triangles Drafting triangles made from highquality aluminum for longterm use without cracking or discoloration The 30 60 90 triangle is special because it forms an equilateral triangle when a mirror image of itself is drawn, meaning all sides are equal!A 30° – 60° – 90° triangle is shown below Find the value of y 30 10 60 y%3D Question This is not a graded question I made this quiz to test how smart this app is, the others got these 2 questions wrong, will you be the one to get the correct answer?




Special Right Triangles Interactive Notebook Page Math Methods Teaching Geometry Teaching Math




30 60 90 Triangle Theorem Ratio Formula Video
A right triangle is a special right triangle in which one angle measures 30 degrees and the other 60 degrees The key characteristic of a right triangle is that its angles have measures of 30 degrees (π/6 rads), 60 degrees (π/3 rads) and 90 degrees (π/2 rads) The sides of a right triangle lie in the ratio 1√32Use this value to label the other two sides of the triangle Use the values on the triangle to find the requested trigonometric values30 60 90 triangle calculator math 30 60 90 triangle in trigonometry It can also provide the calculation steps and how the right triangle looks Right triangle calculator to compute side length angle height area and perimeter of a right triangle given any 2 values Its properties are so special because it s half of the equilateral triangle




30 60 90 Triangle




Special Right Triangles Fully Explained W 19 Examples
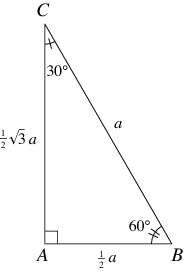
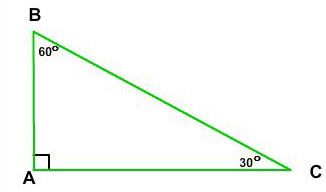
A triangle is a special triangle since the length of its sides is always in a consistent relationship with one another In the belowgiven triangle ABC, ∠ C = 30°, ∠ A = 60°, and ∠ B = 90° We can understand the relationship between eachThe property is that the lengths of the sides of a triangle are in the ratio 12√3 Thus if you know that the side opposite the 60 degree angle measures 5 inches then then this is √3 times as long as the side opposite the 30 degree so the side opposite the 30 degree angle is 5 /A triangle is a special right triangle with some very special characteristics If you have a degree triangle, you can find a missing side length without using the Pythagorean theorem!



Trig Ratios For 30 60 90 Triangles Youtube



Special Right Triangle 30 60 90 Mathbitsnotebook Geo Ccss Math
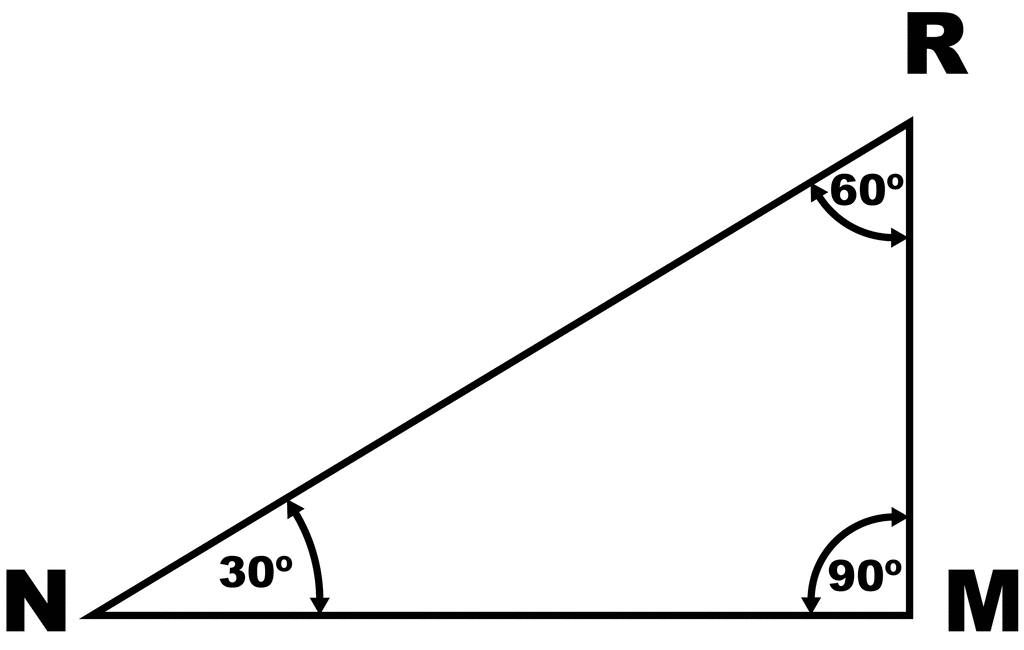
Represents the angle measurements of a right triangle This type of triangle is a scalene right triangle The sides are in the ratio of , with the across from the 30, the as the hypotenuse, and the across from 60 Using variables, it can be written as



Identifying The 30 60 90 Degree Triangle Dummies
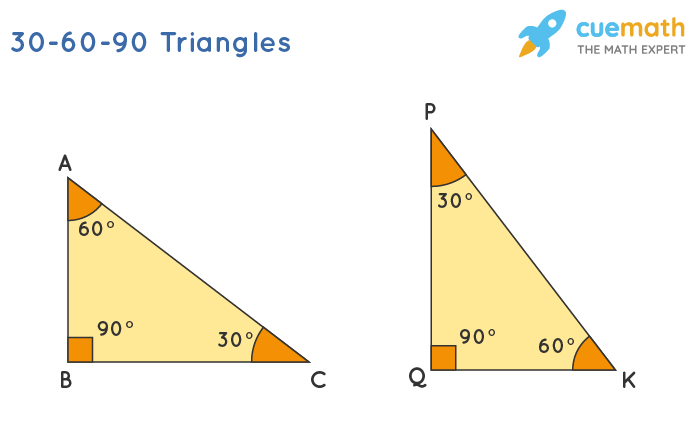



30 60 90 Triangle Definition Theorem Formula Examples




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com
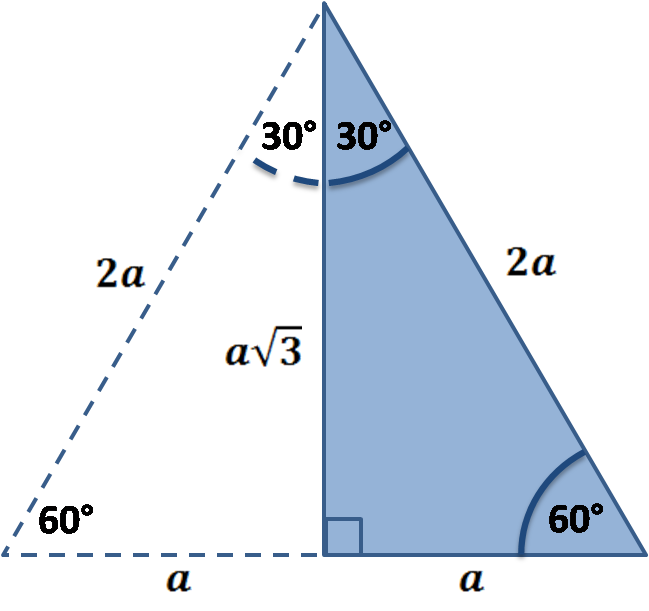



30 60 90 Triangles Blackman High School
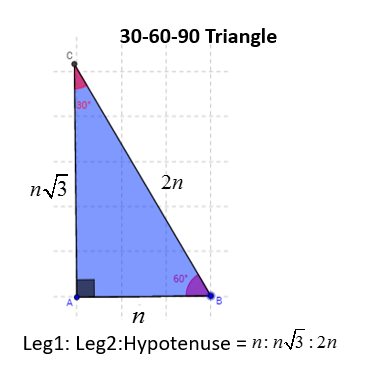



30 60 90 Right Triangles Solutions Examples Videos
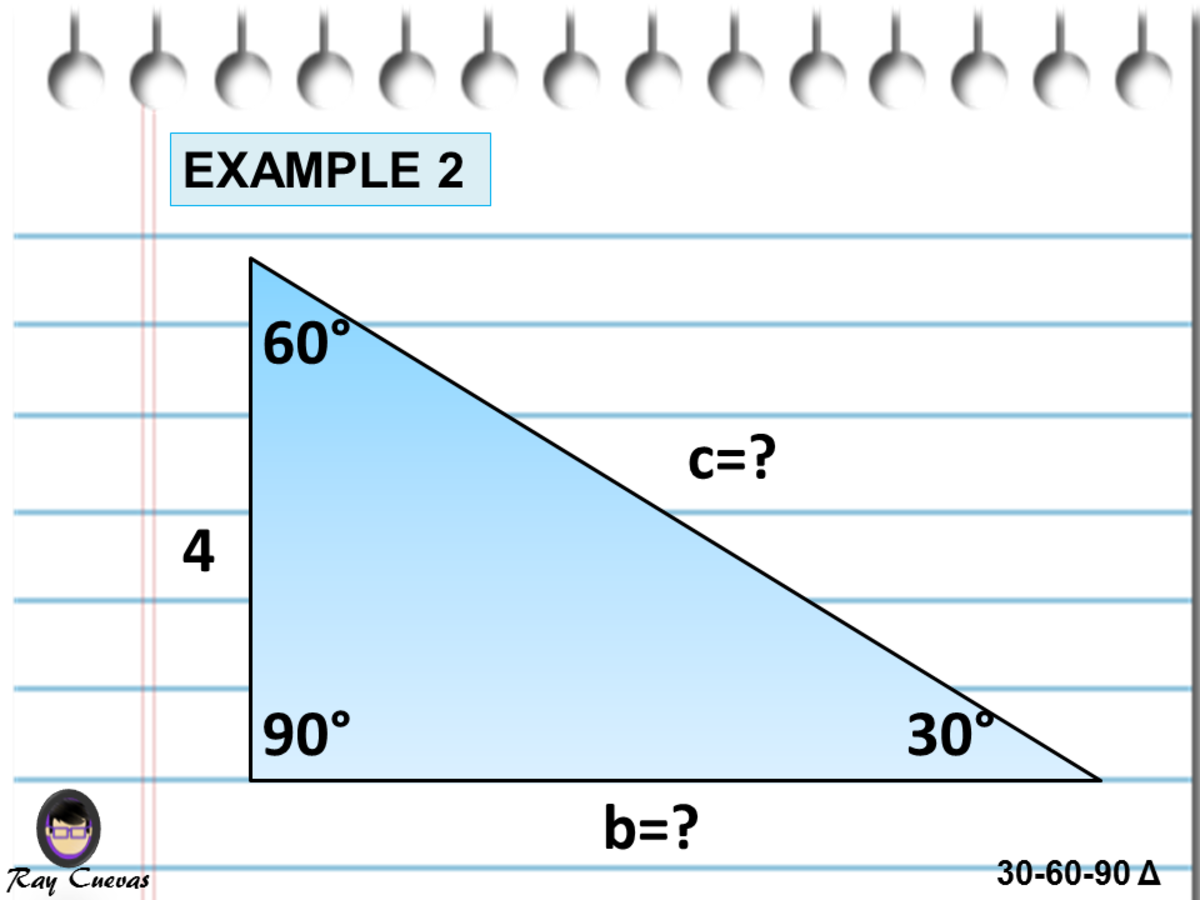



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation



How To Solve 30 60 90 Triangles Krista King Math Online Math Tutor



30 60 90 Triangle Geometry



The Converse Of The Pythagorean Theorem And Special Triangles Geometry Right Triangles And Trigonometry Mathplanet



Triangle 30 60 90 Clipart Etc



30 60 90 Special Right Triangle Calculator Inch Calculator



3
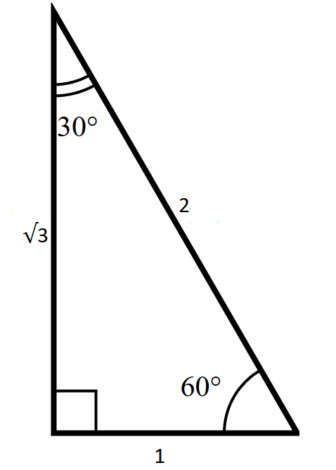



The Complete Guide To The 30 60 90 Triangle



Construct A Triangle 30 60 90 Given The Hypotenuse Technical Graphics
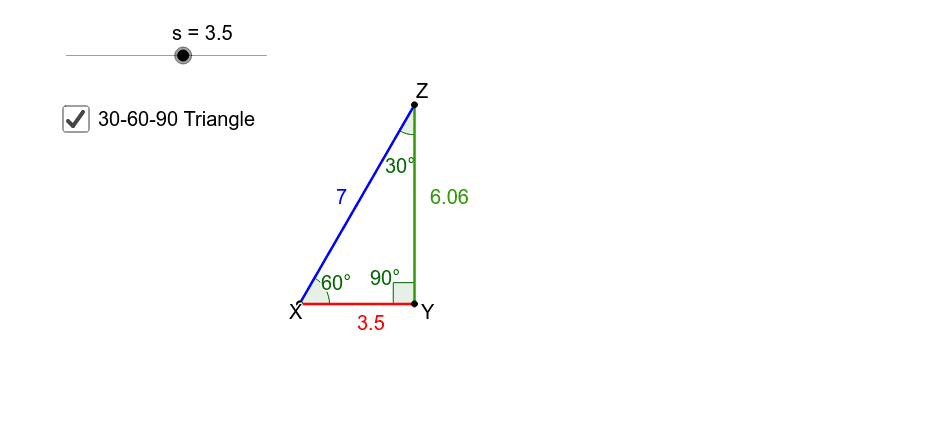



Special Right Triangles 30 60 90 Geogebra
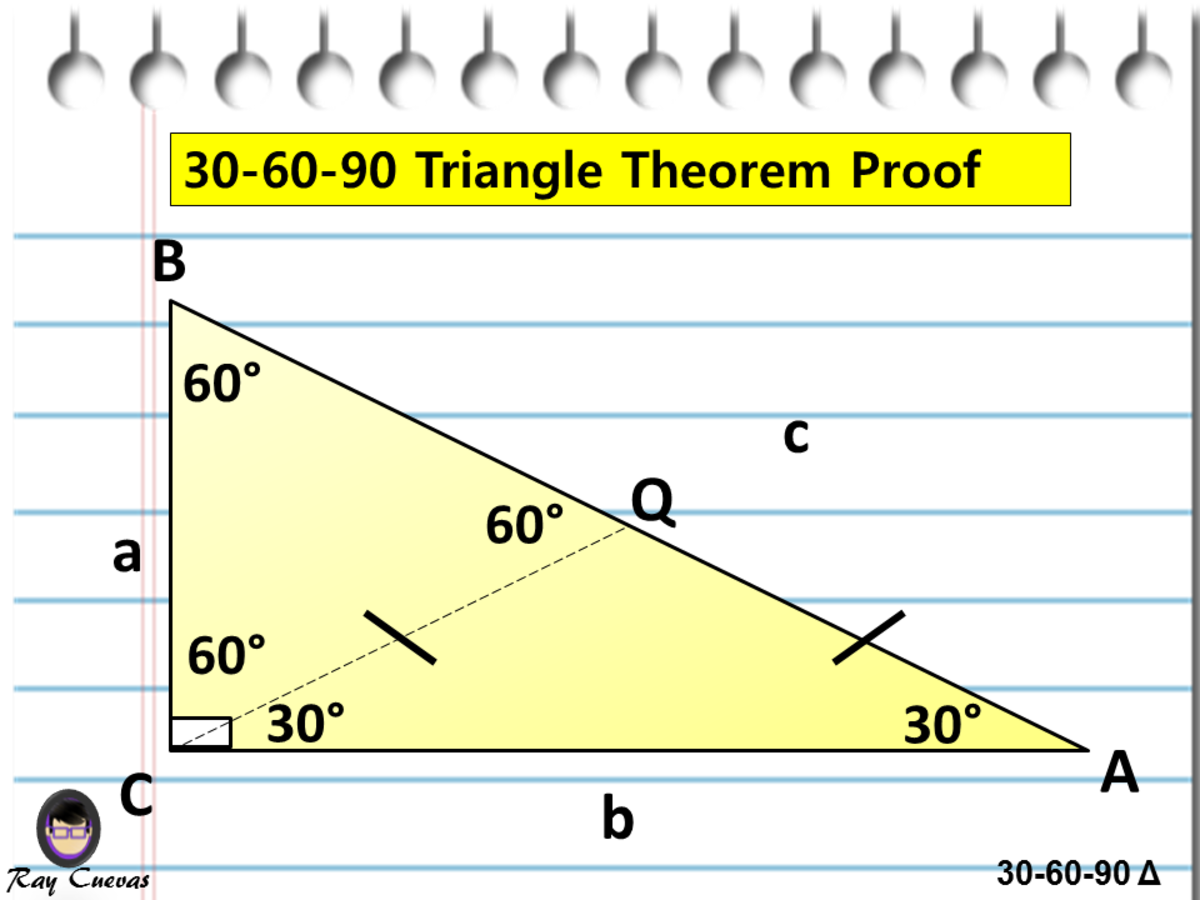



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation




10 30 60 90 Triangle
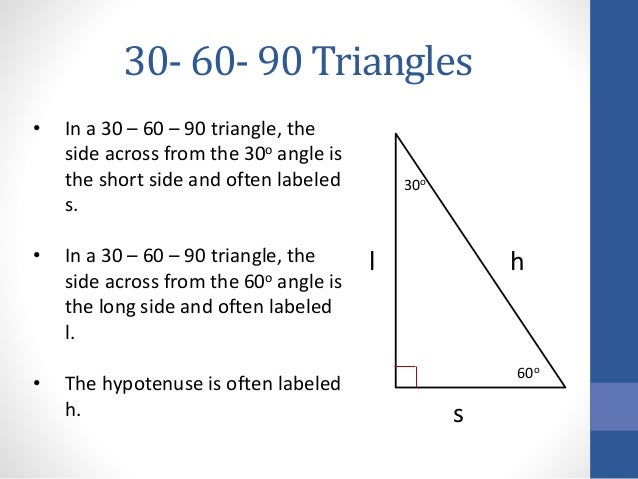



30 60 90 Triangles



30 60 90 Right Triangle Side Ratios Expii



30 60 90 Triangle



A 30 60 90 Triangle Math Central




Relationships Of Sides In 30 60 90 Right Triangles Ck 12 Foundation



Why In A 30 60 90 Triangle Is The The Side Opposite 60 Degrees X Sqrt 3 Quora




30 60 90 Right Triangles Ck 12 Foundation




Woodworker S Triangles Rockler Woodworking Tools




30 60 90 Triangle On The Gmat Article Including Problems



30 60 90 And 45 45 90 Triangle Calculator



30 60 90 Triangle Explanation Examples




30 60 90 Triangle Calculator Formula Rules



30 60 90 Triangle Geometry Help




30 60 90 Triangles Worksheet By Family 2 Family Learning Resources




30 60 90 Right Triangles Consider The Following




How To Construct A 30 60 90 Triangle With Compass And Straightedge Or Ruler Math Open Reference
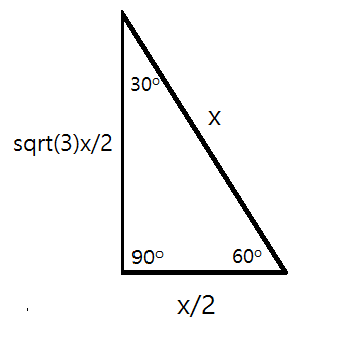



What Is A 30 60 90 Triangle Please Give An Example Socratic
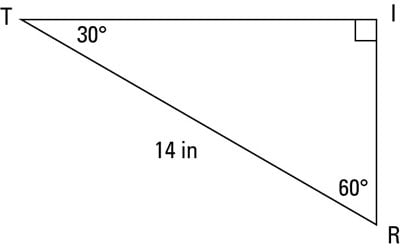



A Quick Guide To The 30 60 90 Degree Triangle Dummies
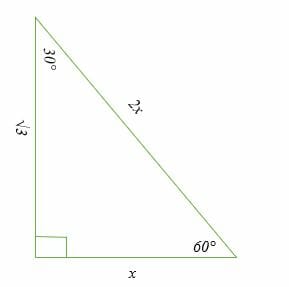



30 60 90 Triangle Explanation Examples




5 30 60 90 Triangles Geometry15a
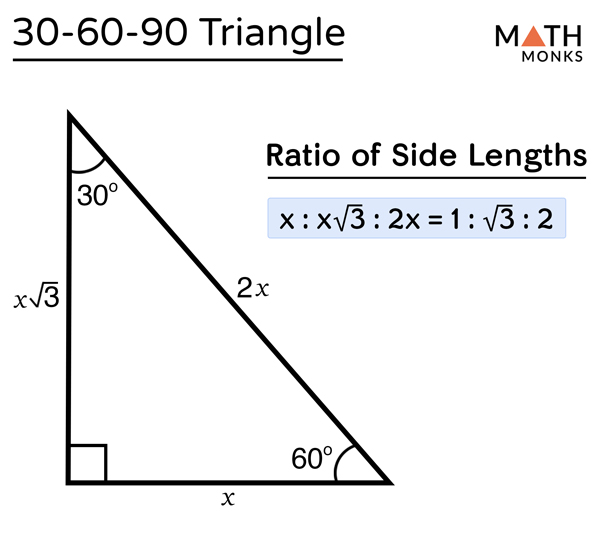



30 60 90 Triangle Definition Formulas Examples




Solved 1 For A 30 60 90 Triangle It Is Known That The Chegg Com



Trig




Activity 22 Construct A 30 60 90 Triangle Geogebra
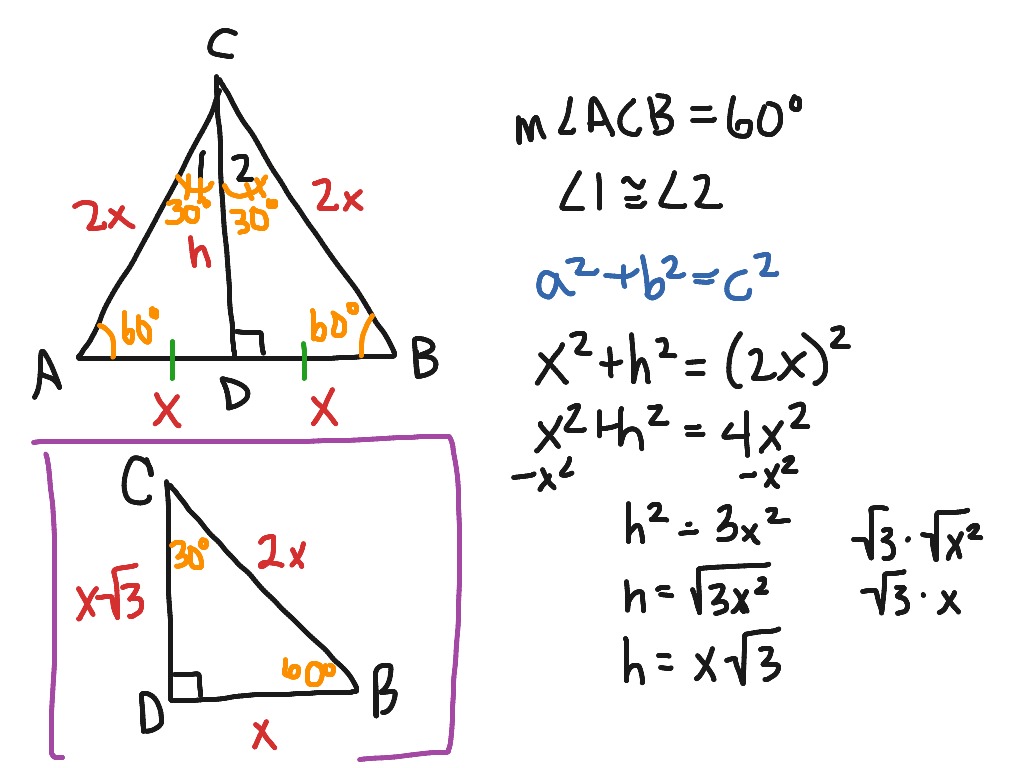



30 60 90 Triangle Math Right Triangles Showme
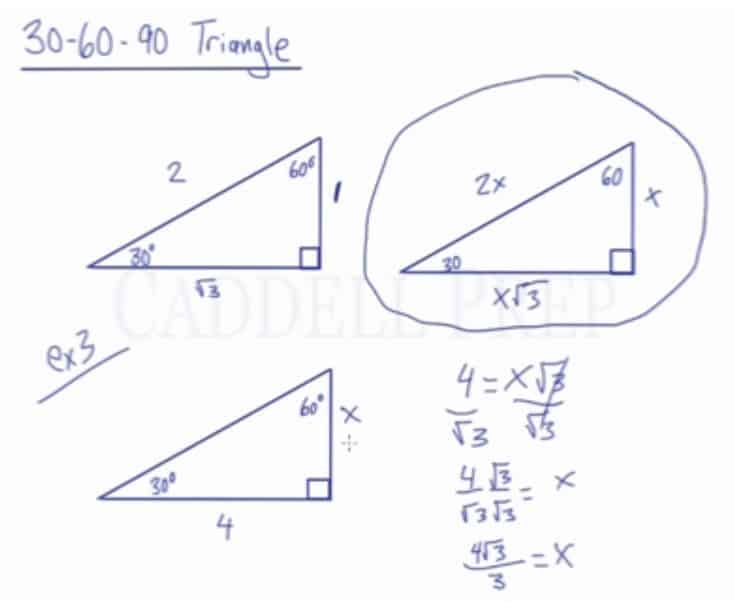



Learn About The 30 60 90 Triangle Caddell Prep Online
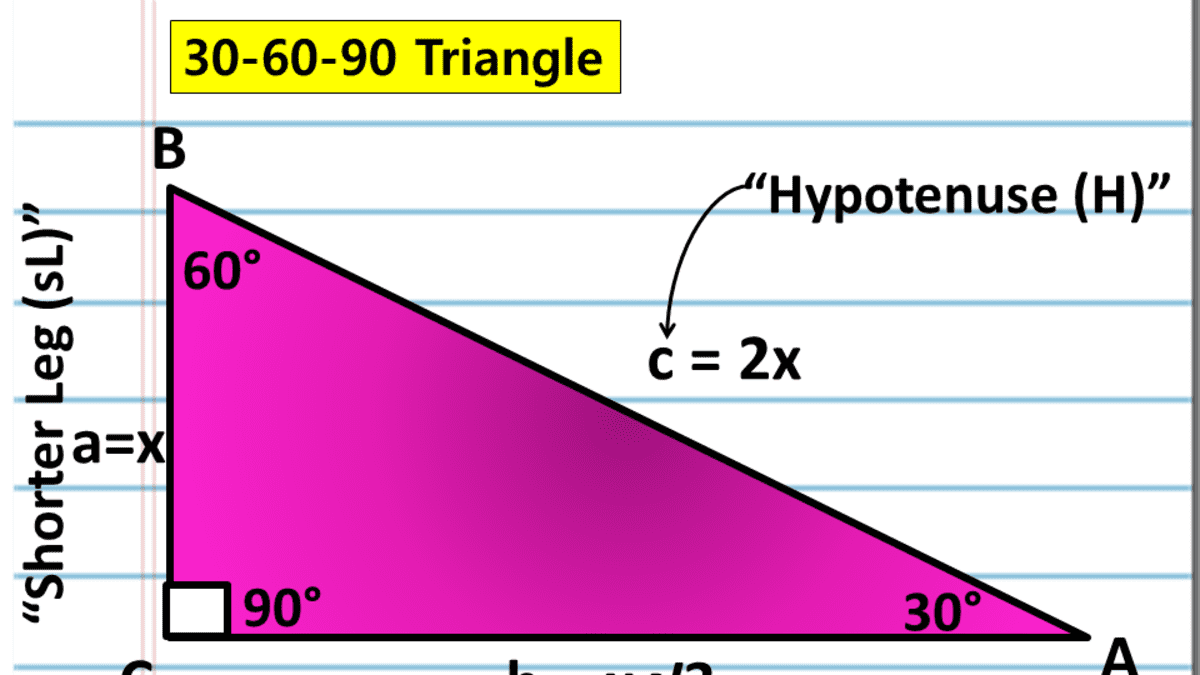



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation



Mrwadeturner 30 60 90 Triangle 6th
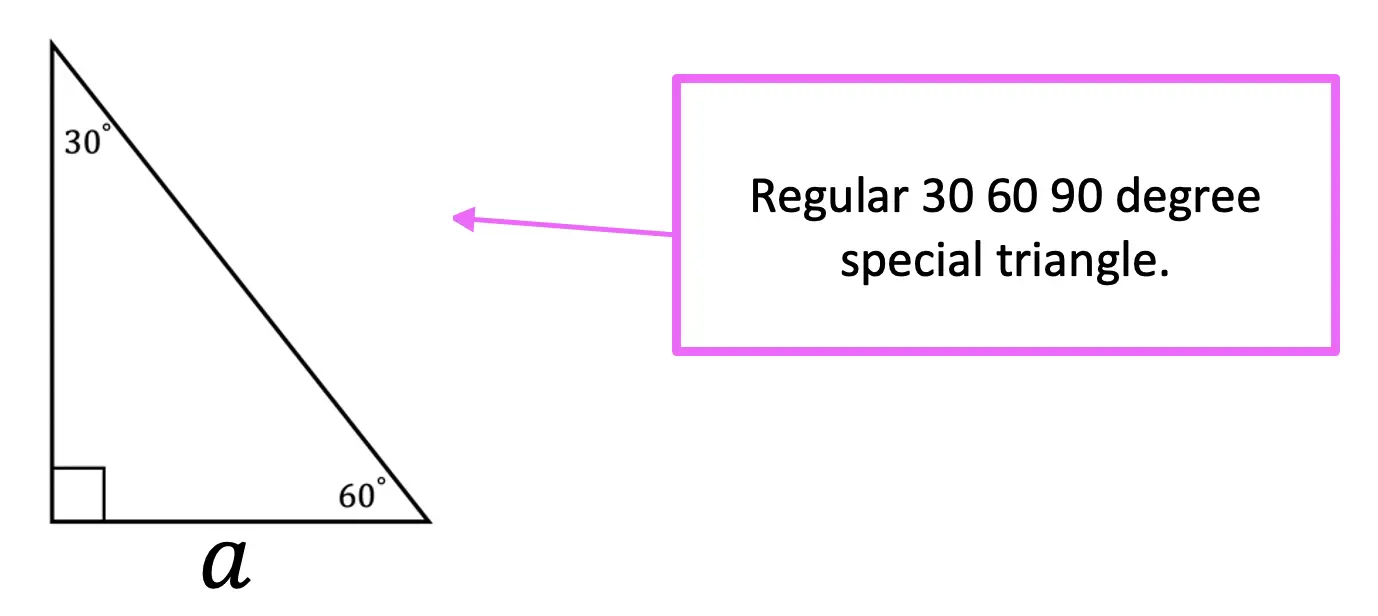



30 60 90 Special Triangles Geometry Mathsux 2



Special Right Triangle 30 60 90 Mathondemand Com




30 60 90 Triangle Theorem Proof Don T Memorise Youtube



The 30 60 90 Triangle Topics In Trigonometry
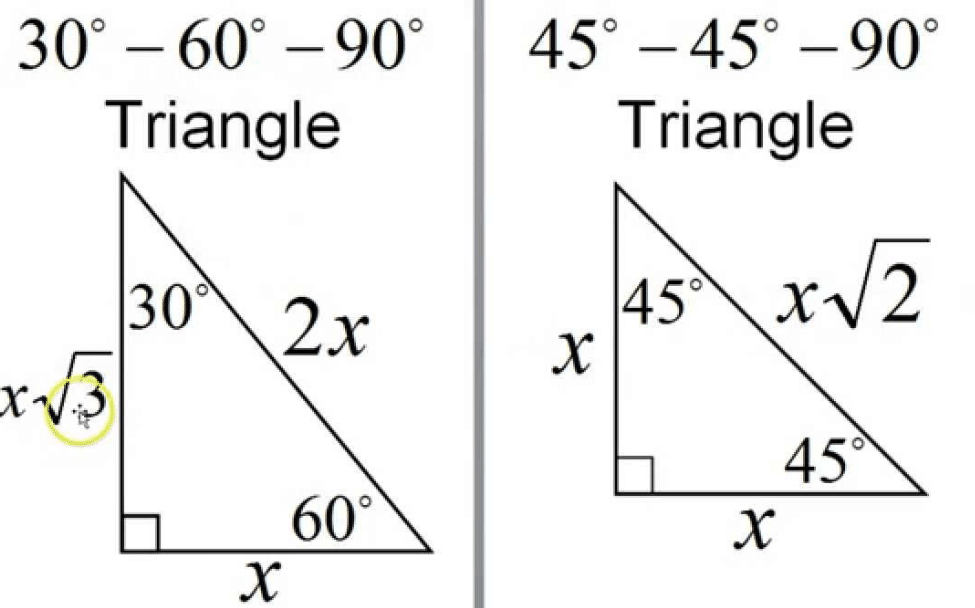



How To Work With 30 60 90 Degree Triangles Education Is Around




Amazon Com C Thru Kt 80 Student 30 60 90 Triangle 9 75 In Musical Instruments




Triangle Gma Is 30 Degree 60 Degree 90 Degree If M 26 Cm Find A And S Study Com



30 60 90 Right Triangle Side Ratios Expii



What Is The Area Of A 30 60 And 90 Triangle If The Hypotenuse Is 12 In Quora



5 5 Special Triangles




To Remember 30 60 90 Triangles One Boy Has An X S One Boy Has 2 X S And The Middle Boy Had 3 X S That He S Still Hung Teaching Materials Teaching Remember




Special Right Triangles Review Article Khan Academy



What Is A 30 60 90 Degree Triangle Virtual Nerd Can Help




Solve For X And Y 30 60 90 Triangles Brainly Com




Special Right Triangles 30 60 90 Ck 12 Foundation



Special Triangles Hiset Math



30 60 90 Triangles



Special Right Triangle 30 60 90 Mathbitsnotebook Geo Ccss Math




Right Triangles 30 60 90 Special Right Triangles Notes And Practice




30 60 90 Triangle Theorem Ratio Formula Video



How To Use The Special Right Triangle 30 60 90 Studypug



Solve A 30 60 90 Triangle With Gradea



File 30 60 90 Triangle Svg Wikipedia



30 60 90 Right Triangle How Do I Solve If The Long Leg Is 10 Socratic



45 45 90 And 30 60 90 Triangles Zona Land Education



A Quick Guide To The 30 60 90 Degree Triangle Dummies




30 60 90 Triangle



1



30 60 90 Triangle Formulas Rules And Sides Science Trends
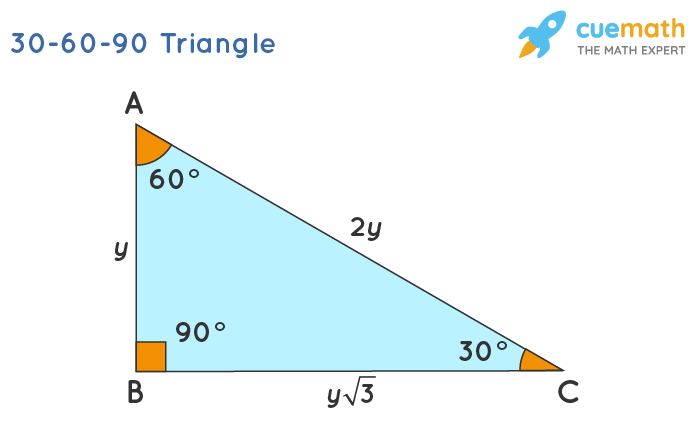



30 60 90 Triangle Definition Theorem Formula Examples




30 60 90 Triangles Spock S Guide To Math 4




C Thru Kt 80 Student 30 60 90 Triangle 9 75 In
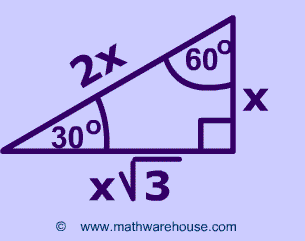



Special Right Triangles Formulas 30 60 90 And 45 45 90 Special Right Triangles Examples Pictures And Practice Problems
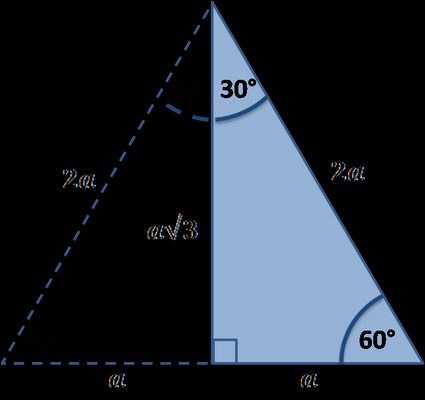



30 60 90 Triangle Calculator Formula Rules




File 30 60 90 Triangle 2 Svg Wikimedia Commons
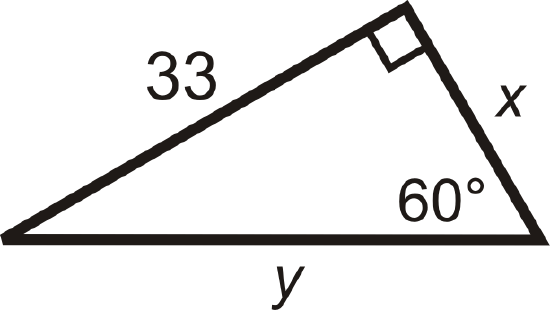



4 43 30 60 90 Right Triangles K12 Libretexts




Ppt 30 60 90 Right Triangles Powerpoint Presentation Free Download Id




Plan View Geometry Of 30 60 90 Triangle For Extrusion Time Saving Download Scientific Diagram
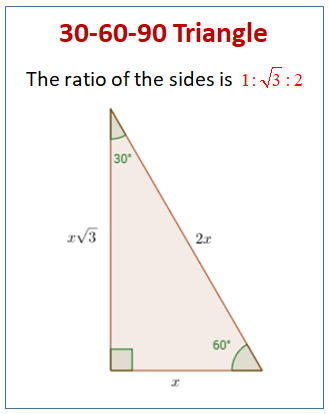



30 60 90 Special Right Triangles Videos Worksheets Examples Solutions
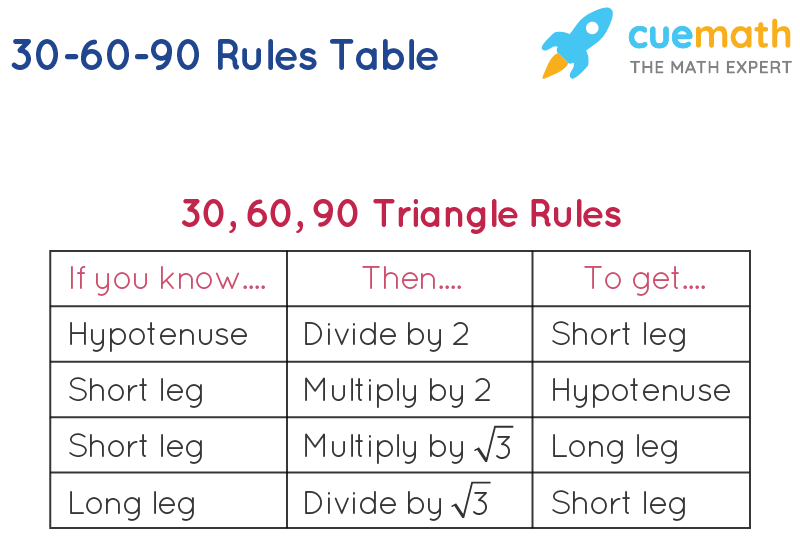



30 60 90 Formula Learn Formula For Calculating The 30 60 90 Measures
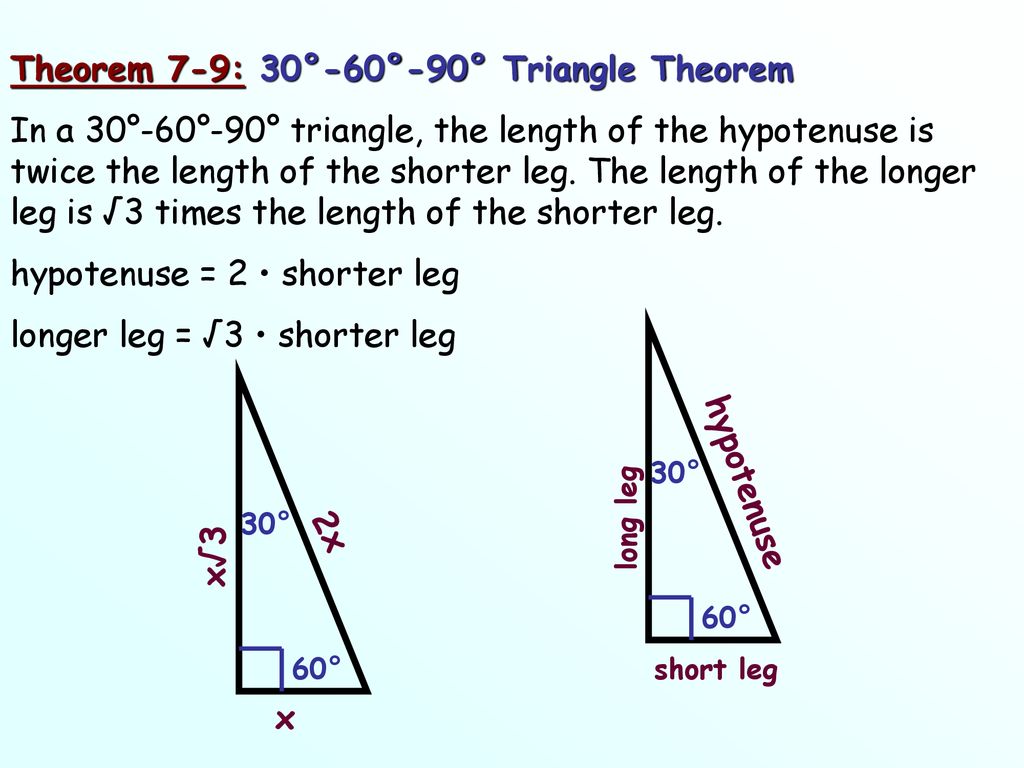



Objective To Use The Properties Of 30 60 90 Triangle Ppt Download



Rockler 30 60 90 Woodworker S Triangle The Woodsmith Store



The Easy Guide To The 30 60 90 Triangle



0 件のコメント:
コメントを投稿